Simulating inelastic neutron scattering
This tutorial implements a simplified and minimal version of the workflow presented in the preprint by Lindgren et al. (2025) for simulating inelastic neutron scattering spectra (INS) from first principles. Specifically, this notebook demonstrates how to run molecular dynamics (MD) simulations using a NEP model for crystalline benzene, compute the INS spectrum from the dynamic structure factor, and correct for the instrument resolution and kinematic constraint in order to compare to experimentally measured spectra. We compare to the INS spectrum measured at the TOSCA spectrometer at the ISIS Neutron and Muon Source in the UK, published in the preprint by Lindgren et al.
For training NEP models, please refer to the tutorial for calorine on the topic, as well as the preprint by Lindgren et al.
In addition to the requirements for calorine, this tutorial requires installation of the following packages:
dynasorLink:pip install dynasoreuphonicLink:pip install euphonicresINSLink: Requires manual installation by cloning the git repository and adding it to yourPYTHONPATH.
This tutorial takes a few minutes to run on a workstation with a decent consumer-grade GPU (Nvidia RTX 3080Ti).
Preparations
We begin by loading a primitive benzene structure in the I phase, and and load the NEP model nep-benzene.txt for crystalline benzene, available from the Zenodo record from Lindgren et al. (2025). Both files are available in the tutorials/ folder in the GitLab repository.
We then use the NEP model to relax the primitive structure.
[1]:
import warnings
from ase.io import read
from calorine.calculators import CPUNEP
from calorine.tools import relax_structure
# ASE raises a warning when reading the orthorombic structure from the .cif file.
# The resulting structure seems to have the correct symmetry and cell, so we suppress the warning.
with warnings.catch_warnings():
warnings.simplefilter("ignore", category=UserWarning)
primitive = read('benzene-I.cif')
potential = './nep-benzene.txt'
calculator = CPUNEP(potential)
primitive.calc = calculator
[2]:
# Relax the structure
epot = primitive.get_potential_energy() / len(primitive)
print(
f"Before relax: potential energy = {epot:.3f} eV/atom", flush=True
)
relax_structure(primitive, minimizer='bfgs-scipy', fmax=1e-3)
epot = primitive.get_potential_energy() / len(primitive)
print(
f"After relax : potential energy = {epot:.3f} eV/atom", flush=True
)
Before relax: potential energy = -5.390 eV/atom
After relax : potential energy = -5.726 eV/atom
Next, we will set up the supercell for molecular dynamics. We will use a relatively small system size for the purpose of this tutorial. Note that the supercell is created such that the cell vectors are approximately of equal length.
[3]:
# Setup the supercell for molecular dynamics
repeats = (4, 3, 4)
supercell = primitive.repeat(repeats)
cell_lengths = supercell.cell.lengths()
print('Number of atoms in supercell:', len(supercell))
print('Cell vector lengths in supercell (Å):', cell_lengths)
Number of atoms in supercell: 2304
Cell vector lengths in supercell (Å): [28.86051953 28.44991489 28.13375907]
Benzene in Phase I has a Pbca (61) spacegroup, which is an orthorombic structure. As the relaxation of the structure above slightly changed this symmetry, we can enforce it by setting the cell vector angles to 90 degrees.
[4]:
from ase.cell import Cell
cell_angles = [90, 90, 90]
new_cell_params = [*cell_lengths, *cell_angles]
new_cell = Cell.new(new_cell_params)
supercell.set_cell(new_cell, scale_atoms=True)
Molecular dynamics
We are now ready to configure the molecular dynamics simulation. The simulation protocol is divided into two parts. First, we perform an equilibration run to get the correct simulation cell at the target conditions of 127 K and a pressure of 0 GPa. From the last few snapshots of the trajectory from the equilibration run we then extract the average simulation cell, and use this cell to perform a production run, where the atomic positions are written with a high frequency of every 3 fs.
This high frequency is required for the next step of the workflow, where we compute the dynamic structure factor. It is paramount to write the sufficiently often, such that all vibrational modes are sampled atleast twice per period accoding to the Nyquist sampling theorem. In our system, the fastest mode is the C-H stretching mode, which has an energy of ~3200 cm\(^{-1}\) or 400 meV, equivalent to a period time of 10.5 fs. Writing the trajectory file ever 3 fs is thus sufficient to respect the Nyquist condition.
[5]:
%%time
from typing import List
from os.path import isfile
from pathlib import Path
from calorine.calculators import GPUNEP
time_step = 0.1 # fs
elastic_tensor = [40, 40, 40] # rough estimate of elastic tensor, in GPa
pressure = [0, 0, 0] # pressure tensor, in GPa
temperature = 127 # K
# Assign the supercell a GPU calculator to run the MD on the GPU
gpumd_command = "gpumd 2>&1" # Write all output from GPUMD to stdout
gpu_calculator = GPUNEP(potential, command=gpumd_command)
supercell.calc = gpu_calculator
def run_inference(calculator: GPUNEP, parameters: List, label: str):
directory_exists = False
directory = f"./{label}"
try:
Path(f"./{label}").mkdir(exist_ok=False)
print(directory, flush=True)
except FileExistsError:
directory_exists = True
print(f"{label} already exists", flush=True)
if directory_exists:
dump = f"{directory}/dump.xyz"
out_exists = isfile(dump)
if out_exists:
print("Job completed, continuing to next step", flush=True)
return
calculator.set_directory(str(directory))
calculator.run_custom_md(parameters)
def equilibration(gpu_calculator: GPUNEP, time_step: int, temperature: int, pressure: List, elastic_tensor: List):
equilibration_params = [
("time_step", time_step),
("velocity", temperature),
("ensemble", ("nvt_ber", temperature, temperature, 100)),
("dump_thermo", 100),
("run", int(1e4)), # 1 ps
(
"ensemble",
("npt_scr", temperature, temperature, 100, *pressure, *elastic_tensor, 200),
),
("dump_thermo", 100),
("run", int(1e4)), # 1 ps
(
"ensemble",
("npt_scr", temperature, temperature, 100, *pressure, *elastic_tensor, 200),
),
("dump_thermo", 100),
("dump_restart", 100),
("dump_exyz", (100, 0, 0)),
("run", int(1e4)), # Run a last simulation to extract the average volume
]
run_inference(gpu_calculator, equilibration_params, label="equilibration")
equilibration(gpu_calculator, time_step, temperature, pressure, elastic_tensor)
./equilibration
***************************************************************
* Welcome to use GPUMD *
* (Graphics Processing Units Molecular Dynamics) *
* version 4.0 *
* This is the gpumd executable *
***************************************************************
---------------------------------------------------------------
Compiling options:
---------------------------------------------------------------
DEBUG is on: Use a fixed PRNG seed for different runs.
---------------------------------------------------------------
GPU information:
---------------------------------------------------------------
number of GPUs = 1
Device id: 0
Device name: NVIDIA GeForce RTX 3080 Ti
Compute capability: 8.6
Amount of global memory: 11.6237 GB
Number of SMs: 80
---------------------------------------------------------------
Started running GPUMD.
---------------------------------------------------------------
---------------------------------------------------------------
Started initializing positions and related parameters.
---------------------------------------------------------------
Number of atoms is 2304.
Use periodic boundary conditions along x.
Use periodic boundary conditions along y.
Use periodic boundary conditions along z.
Box matrix h = [a, b, c] is
2.8860519529e+01 0.0000000000e+00 0.0000000000e+00
0.0000000000e+00 2.8449914887e+01 0.0000000000e+00
0.0000000000e+00 0.0000000000e+00 2.8133759074e+01
Inverse box matrix g = inv(h) is
3.4649410901e-02 0.0000000000e+00 0.0000000000e+00
0.0000000000e+00 3.5149490042e-02 0.0000000000e+00
0.0000000000e+00 0.0000000000e+00 3.5544485803e-02
Do not specify initial velocities here.
Have no grouping method.
There are 2 atom types.
1152 atoms of type 0.
1152 atoms of type 1.
Initialized velocities with default T = 300 K.
---------------------------------------------------------------
Finished initializing positions and related parameters.
---------------------------------------------------------------
---------------------------------------------------------------
Started executing the commands in run.in.
---------------------------------------------------------------
Use the NEP4 potential with 2 atom types.
type 0 (C with Z = 6).
type 1 (H with Z = 1).
has the universal ZBL with inner cutoff 0.5 A and outer cutoff 1 A.
radial cutoff = 8 A.
angular cutoff = 4 A.
MN_radial = 374.
enlarged MN_radial = 468.
enlarged MN_angular = 68.
n_max_radial = 8.
n_max_angular = 6.
basis_size_radial = 12.
basis_size_angular = 12.
l_max_3body = 4.
l_max_4body = 2.
l_max_5body = 0.
ANN = 44-50-1.
number of neural network parameters = 4601.
number of descriptor parameters = 832.
total number of parameters = 5433.
Time step for this run is 0.1 fs.
Initialized velocities with input T = 127 K.
Use NVT ensemble for this run.
choose the Berendsen method.
initial temperature is 127 K.
final temperature is 127 K.
tau_T is 100 time_step.
Dump thermo every 100 steps.
Run 10000 steps.
1000 steps completed.
2000 steps completed.
3000 steps completed.
4000 steps completed.
5000 steps completed.
6000 steps completed.
7000 steps completed.
8000 steps completed.
9000 steps completed.
10000 steps completed.
---------------------------------------------------------------
Time used for this run = 39.2844 second.
Speed of this run = 586493 atom*step/second.
---------------------------------------------------------------
Use NPT ensemble for this run.
choose the SCR method.
initial temperature is 127 K.
final temperature is 127 K.
tau_T is 100 time_step.
pressure_xx is 0 GPa.
pressure_yy is 0 GPa.
pressure_zz is 0 GPa.
modulus_xx is 40 GPa.
modulus_yy is 40 GPa.
modulus_zz is 40 GPa.
tau_p is 200 time_step.
Dump thermo every 100 steps.
Run 10000 steps.
1000 steps completed.
2000 steps completed.
3000 steps completed.
4000 steps completed.
5000 steps completed.
6000 steps completed.
7000 steps completed.
8000 steps completed.
9000 steps completed.
10000 steps completed.
---------------------------------------------------------------
Time used for this run = 38.9186 second.
Speed of this run = 592004 atom*step/second.
---------------------------------------------------------------
Use NPT ensemble for this run.
choose the SCR method.
initial temperature is 127 K.
final temperature is 127 K.
tau_T is 100 time_step.
pressure_xx is 0 GPa.
pressure_yy is 0 GPa.
pressure_zz is 0 GPa.
modulus_xx is 40 GPa.
modulus_yy is 40 GPa.
modulus_zz is 40 GPa.
tau_p is 200 time_step.
Dump thermo every 100 steps.
Dump restart every 100 steps.
---------------------------------------------------------------
Warning: Starting from GPUMD-v3.4, the velocity data in restart.xyz will be in units of Angstrom/fs
Previously they are in units of 1/1.018051e+1 Angstrom/fs.
---------------------------------------------------------------
Dump extended XYZ.
every 100 steps.
without velocity data.
without force data.
Run 10000 steps.
1000 steps completed.
2000 steps completed.
3000 steps completed.
4000 steps completed.
5000 steps completed.
6000 steps completed.
7000 steps completed.
8000 steps completed.
9000 steps completed.
10000 steps completed.
---------------------------------------------------------------
Time used for this run = 39.213 second.
Speed of this run = 587560 atom*step/second.
---------------------------------------------------------------
---------------------------------------------------------------
Finished executing the commands in run.in.
---------------------------------------------------------------
---------------------------------------------------------------
Time used = 117.419010 s.
---------------------------------------------------------------
---------------------------------------------------------------
Finished running GPUMD.
---------------------------------------------------------------
CPU times: user 672 ms, sys: 4.05 ms, total: 676 ms
Wall time: 1min 57s
We quickly check the thermo.out file to ensure that the structure is properly equilibrated before we move on to production.
[6]:
import numpy as np
from calorine.gpumd.io import read_thermo
import matplotlib.pyplot as plt
N_atoms = len(supercell)
thermo = read_thermo('equilibration/thermo.out', natoms=N_atoms)
time = np.linspace(0, len(thermo)*10, len(thermo)) # in fs, thermo is written every 100 steps = 10 fs
fig, axes = plt.subplots(figsize=(3.3, 5), nrows=4, sharex=True, dpi=200)
# Potential energy
ax = axes[0]
ax.plot(time, thermo['potential_energy'])
ax.set_ylabel('Potential\nenergy (eV/atom)')
# Temperature
ax = axes[1]
ax.plot(time, thermo['temperature'])
ax.set_ylabel('Temperature (K)')
# Cell volume
ax = axes[2]
a = np.array(thermo["cell_xx"])
b = np.array(thermo["cell_yy"])
c = np.array(thermo["cell_zz"])
V = a * b * c
ax.plot(time, a / repeats[0])
ax.plot(time, b / repeats[1])
ax.plot(time, c / repeats[2])
ax.set_ylabel('Volume (Å$^3$)')
# Pressure
ax = axes[3]
P = -1 / 3 * (thermo["stress_xx"] + thermo["stress_yy"] + thermo["stress_zz"])
ax.plot(time, P)
ax.set_ylabel('Pressure (GPa)')
ax.set_xlabel('Time (fs)')
plt.tight_layout()
plt.subplots_adjust(wspace=0, hspace=0)
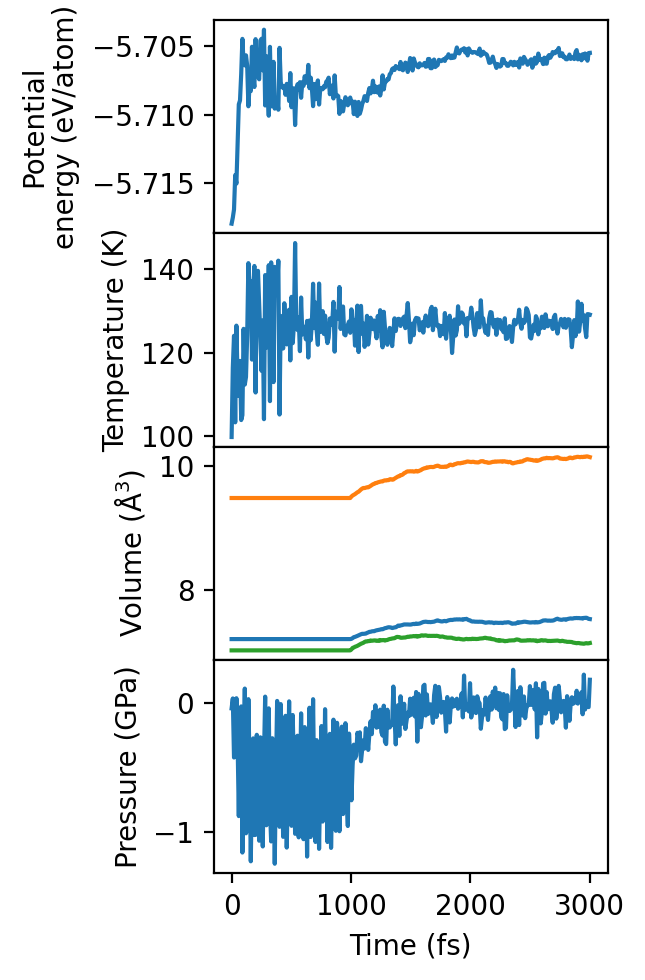
As we can see, the simulation is barely equilibrated after 3 ps of total simulation. For an accurate, paper-grade simulation one should to equilibrate for probably one or two orders of magnitude longer. For the purposes of this tutorial, however, it suffices.
We now extract the last 50 frames, and extract the equilibrated cell vectors.
[7]:
def extract_average_cell(trajectory, supercell):
"""
Reads the last 100 frames of a trajectory and computes the average cell.
For systems with known symmetry, the cell is formatted to correctly obey
the symmetry.
"""
structures = read("./equilibration/dump.xyz", ":")[-50:]
angles = np.array([s.cell.angles() for s in structures])
lengths = np.array([s.cell.lengths() for s in structures])
avg_lengths = np.mean(lengths, axis=0)
avg_angles = np.mean(angles, axis=0)
# Benzene is orthorombic
cell_lengths = avg_lengths
cell_angles = np.array([90, 90, 90])
print(f"Lattice vectors: {supercell.cell.lengths()} -> {cell_lengths}", flush=True)
print(f"Cell angles: {supercell.cell.angles()} -> {cell_angles}", flush=True)
new_cell_params = [*cell_lengths, *cell_angles]
new_cell = Cell.new(new_cell_params)
return new_cell
new_cell = extract_average_cell("./equlibration/dump.xyz", supercell)
relaxed = supercell.copy()
relaxed.set_cell(new_cell, scale_atoms=True) # set average cell
relaxed.wrap() # Make sure atoms are wrapped into the simulation cell
Lattice vectors: [28.86051953 28.44991489 28.13375907] -> [30.10346547 30.36847412 28.6982577 ]
Cell angles: [90. 90. 90.] -> [90 90 90]
Now, we can run a production run, in the microcanonic (NVE) ensemble. The NVE ensemble is suitable for production as there is no interference on the dynamics of the atoms from a thermostat or barostat.
We will equilibrate the system quickly in the NVT ensemble for 1 ps, and then transition to the NVE ensemble where positions are written every 3 fs.
[8]:
%%time
def production(gpu_calculator: GPUNEP, time_step: int, temperature: int, pressure: List, elastic_tensor: List):
equilibration_params = [
("time_step", time_step),
("velocity", temperature),
("ensemble", ("nvt_bdp", temperature, temperature, 100)),
("dump_thermo", 100),
("dump_restart", 100),
("run", int(1e4)),
("ensemble", "nve"),
("dump_thermo", 100),
("dump_restart", 100),
("dump_exyz", (30, 0, 0)), # Write trajectory ever 3 fs
("run", int(4e4)),
]
run_inference(gpu_calculator, equilibration_params, label="production")
production_calculator = GPUNEP(potential, command=gpumd_command)
relaxed.calc = production_calculator
production(production_calculator, time_step, temperature, pressure, elastic_tensor)
./production
***************************************************************
* Welcome to use GPUMD *
* (Graphics Processing Units Molecular Dynamics) *
* version 4.0 *
* This is the gpumd executable *
***************************************************************
---------------------------------------------------------------
Compiling options:
---------------------------------------------------------------
DEBUG is on: Use a fixed PRNG seed for different runs.
---------------------------------------------------------------
GPU information:
---------------------------------------------------------------
number of GPUs = 1
Device id: 0
Device name: NVIDIA GeForce RTX 3080 Ti
Compute capability: 8.6
Amount of global memory: 11.6237 GB
Number of SMs: 80
---------------------------------------------------------------
Started running GPUMD.
---------------------------------------------------------------
---------------------------------------------------------------
Started initializing positions and related parameters.
---------------------------------------------------------------
Number of atoms is 2304.
Use periodic boundary conditions along x.
Use periodic boundary conditions along y.
Use periodic boundary conditions along z.
Box matrix h = [a, b, c] is
3.0103465473e+01 0.0000000000e+00 0.0000000000e+00
0.0000000000e+00 3.0368474118e+01 0.0000000000e+00
0.0000000000e+00 0.0000000000e+00 2.8698257703e+01
Inverse box matrix g = inv(h) is
3.3218766820e-02 0.0000000000e+00 0.0000000000e+00
0.0000000000e+00 3.2928885268e-02 0.0000000000e+00
0.0000000000e+00 0.0000000000e+00 3.4845320937e-02
Do not specify initial velocities here.
Have no grouping method.
There are 2 atom types.
1152 atoms of type 0.
1152 atoms of type 1.
Initialized velocities with default T = 300 K.
---------------------------------------------------------------
Finished initializing positions and related parameters.
---------------------------------------------------------------
---------------------------------------------------------------
Started executing the commands in run.in.
---------------------------------------------------------------
Use the NEP4 potential with 2 atom types.
type 0 (C with Z = 6).
type 1 (H with Z = 1).
has the universal ZBL with inner cutoff 0.5 A and outer cutoff 1 A.
radial cutoff = 8 A.
angular cutoff = 4 A.
MN_radial = 374.
enlarged MN_radial = 468.
enlarged MN_angular = 68.
n_max_radial = 8.
n_max_angular = 6.
basis_size_radial = 12.
basis_size_angular = 12.
l_max_3body = 4.
l_max_4body = 2.
l_max_5body = 0.
ANN = 44-50-1.
number of neural network parameters = 4601.
number of descriptor parameters = 832.
total number of parameters = 5433.
Time step for this run is 0.1 fs.
Initialized velocities with input T = 127 K.
Use NVT ensemble for this run.
choose the Bussi-Donadio-Parrinello method.
initial temperature is 127 K.
final temperature is 127 K.
tau_T is 100 time_step.
Dump thermo every 100 steps.
Dump restart every 100 steps.
---------------------------------------------------------------
Warning: Starting from GPUMD-v3.4, the velocity data in restart.xyz will be in units of Angstrom/fs
Previously they are in units of 1/1.018051e+1 Angstrom/fs.
---------------------------------------------------------------
Run 10000 steps.
1000 steps completed.
2000 steps completed.
3000 steps completed.
4000 steps completed.
5000 steps completed.
6000 steps completed.
7000 steps completed.
8000 steps completed.
9000 steps completed.
10000 steps completed.
---------------------------------------------------------------
Time used for this run = 38.1584 second.
Speed of this run = 603800 atom*step/second.
---------------------------------------------------------------
Use NVE ensemble for this run.
Dump thermo every 100 steps.
Dump restart every 100 steps.
---------------------------------------------------------------
Warning: Starting from GPUMD-v3.4, the velocity data in restart.xyz will be in units of Angstrom/fs
Previously they are in units of 1/1.018051e+1 Angstrom/fs.
---------------------------------------------------------------
Dump extended XYZ.
every 30 steps.
without velocity data.
without force data.
Run 40000 steps.
4000 steps completed.
8000 steps completed.
12000 steps completed.
16000 steps completed.
20000 steps completed.
24000 steps completed.
28000 steps completed.
32000 steps completed.
36000 steps completed.
40000 steps completed.
---------------------------------------------------------------
Time used for this run = 153.081 second.
Speed of this run = 602036 atom*step/second.
---------------------------------------------------------------
---------------------------------------------------------------
Finished executing the commands in run.in.
---------------------------------------------------------------
---------------------------------------------------------------
Time used = 191.241763 s.
---------------------------------------------------------------
---------------------------------------------------------------
Finished running GPUMD.
---------------------------------------------------------------
CPU times: user 20.5 ms, sys: 4 ms, total: 24.5 ms
Wall time: 3min 11s
Compute the dynamic structure factor
We now compute the dynamic structure factor \(S(q, \omega)\) using dynasor. The dynamic structure factor is directly proportional to the intensity measured in a scattering experiment, and can be compared to experimental measurements by weighting with appropriate scattering lengths or structure factors.
First, we need to generate the \(q\)-points at which to evaluate the dynamic structure factor. We generate 1000 randomly selected \(q\)-points up to a maximum value of \(q_{max}=12\) rad/Å. This range of \(q\) values is suitable for the specific neutron spectrometer we will compare the simulated spectra to, the TOSCA spectrometer at the ISIS Neutron and Muon Source in the UK.
[9]:
from dynasor.logging_tools import set_logging_level
from dynasor.qpoints import get_spherical_qpoints
from dynasor.sample import DynamicSample
set_logging_level("DEBUG") # Change the dynasor logger level to write debug info to stdout
q_max = 12
q_points = get_spherical_qpoints(relaxed.cell, q_max, max_points=1000)
INFO 2025-06-24 16:52:36: Pruning q-points from the range 0.252 < |q| < 12
INFO 2025-06-24 16:52:36: Pruned from 765641 q-points to 992
We can now compute the dynamic structure factor using the compute_dynamic_structure_factors function. Please refer to the documentation and tutorials available for dynasor for further details.
[10]:
%%time
from dynasor.correlation_functions import compute_dynamic_structure_factors
from dynasor.trajectory import Trajectory
time_window = 1000 # Consider time correlations up to TIME_WINDOW trajectory frames
stride = 50 # Only use every 50th frame to speed up the calculation
dt = 3.0 # dumped every 3fs
frame_step = 1 # read each subsequent frame in the trajectory
max_frames = None # 1 ns
atomic_indices = relaxed.symbols.indices()
trajectory = "./production/dump.xyz"
def compute_dynamic_structure_factor(trajectory_file, atomic_indices: List, time_window: int, stride: int, dt: float, frame_step: int, max_frames: int):
"""Computes the dynamic structure factor using Dynasor."""
traj = Trajectory(
trajectory_file,
trajectory_format="extxyz",
frame_stop=max_frames,
frame_step=frame_step,
atomic_indices=atomic_indices,
)
sample = compute_dynamic_structure_factors(
traj,
q_points,
dt=dt,
window_size=time_window,
window_step=stride,
calculate_incoherent=True,
)
return sample
sample = compute_dynamic_structure_factor(trajectory, atomic_indices, time_window, stride, dt, frame_step, max_frames)
DEBUG 2025-06-24 16:52:36: Using trajectory reader: ExtxyzTrajectoryReader
INFO 2025-06-24 16:52:36: Trajectory file: ./production/dump.xyz
INFO 2025-06-24 16:52:36: Total number of particles: 2304
INFO 2025-06-24 16:52:36: Number of atom types: 2
INFO 2025-06-24 16:52:36: Number of atoms of type C: 1152
INFO 2025-06-24 16:52:36: Number of atoms of type H: 1152
INFO 2025-06-24 16:52:36: Simulation cell (in Angstrom):
[[30.10346547 0. 0. ]
[ 0. 30.36847412 0. ]
[ 0. 0. 28.6982577 ]]
INFO 2025-06-24 16:52:36: Spacing between samples (frame_step): 1
INFO 2025-06-24 16:52:36: Time between consecutive frames in input trajectory (dt): 3.0 fs
INFO 2025-06-24 16:52:36: Time between consecutive frames used (dt * frame_step): 3.0 fs
INFO 2025-06-24 16:52:36: Time window size (dt * frame_step * window_size): 3000.0 fs
INFO 2025-06-24 16:52:36: Angular frequency resolution: dw = 0.001047 rad/fs = 0.689 meV
INFO 2025-06-24 16:52:36: Maximum angular frequency (dw * window_size): 1.047198 rad/fs = 689.278 meV
INFO 2025-06-24 16:52:36: Nyquist angular frequency (2pi / frame_step / dt / 2): 1.047198 rad/fs = 689.278 meV
INFO 2025-06-24 16:52:36: Calculating incoherent part (self-part) of correlations
INFO 2025-06-24 16:52:36: Number of q-points: 992
DEBUG 2025-06-24 16:52:36: Considering pairs:
DEBUG 2025-06-24 16:52:36: ('C', 'C')
DEBUG 2025-06-24 16:52:36: ('C', 'H')
DEBUG 2025-06-24 16:52:36: ('H', 'H')
DEBUG 2025-06-24 16:52:40: Processing window 0 to 1000
INFO 2025-06-24 16:52:40: Processing window 0 to 1000
DEBUG 2025-06-24 16:52:42: Processing window 50 to 1050
DEBUG 2025-06-24 16:52:43: Processing window 100 to 1100
DEBUG 2025-06-24 16:52:45: Processing window 150 to 1150
DEBUG 2025-06-24 16:52:46: Processing window 200 to 1200
DEBUG 2025-06-24 16:52:48: Processing window 250 to 1250
DEBUG 2025-06-24 16:52:49: Processing window 300 to 1300
DEBUG 2025-06-24 16:52:51: Processing window 350 to 1332
DEBUG 2025-06-24 16:52:52: Processing window 400 to 1332
DEBUG 2025-06-24 16:52:53: Processing window 450 to 1332
DEBUG 2025-06-24 16:52:55: Processing window 500 to 1332
DEBUG 2025-06-24 16:52:56: Processing window 550 to 1332
DEBUG 2025-06-24 16:52:57: Processing window 600 to 1332
DEBUG 2025-06-24 16:52:58: Processing window 650 to 1332
DEBUG 2025-06-24 16:52:59: Processing window 700 to 1332
DEBUG 2025-06-24 16:53:00: Processing window 750 to 1332
DEBUG 2025-06-24 16:53:00: Processing window 800 to 1332
DEBUG 2025-06-24 16:53:01: Processing window 850 to 1332
DEBUG 2025-06-24 16:53:02: Processing window 900 to 1332
DEBUG 2025-06-24 16:53:02: Processing window 950 to 1332
DEBUG 2025-06-24 16:53:03: Processing window 1000 to 1332
INFO 2025-06-24 16:53:03: Processing window 1000 to 1332
DEBUG 2025-06-24 16:53:03: Processing window 1050 to 1332
DEBUG 2025-06-24 16:53:04: Processing window 1100 to 1332
DEBUG 2025-06-24 16:53:04: Processing window 1150 to 1332
DEBUG 2025-06-24 16:53:04: Processing window 1200 to 1332
DEBUG 2025-06-24 16:53:04: Processing window 1250 to 1332
DEBUG 2025-06-24 16:53:05: Processing window 1300 to 1332
CPU times: user 11min 37s, sys: 7.32 s, total: 11min 44s
Wall time: 31.2 s
Finally, we compute and apply neutron scattering lengths to the dynamic structure factor in our Sample object, and perform a spherical average over the q-points. The averaging is performed by applying a Gaussian smearing, here with a width of 0.01 rad/Å, to the \(q\)-points.
[11]:
from dynasor.post_processing import (
NeutronScatteringLengths,
get_weighted_sample,
get_spherically_averaged_sample_smearing,
)
def weight_and_average_sample(sample, q_max: float, q_width: float, n_points: int):
"""
Weights a dynasor sample with neutron scattering lengths, and then
performs a spherical averaging in q by applying a Gaussian smearing.
Returns a weighted Dynasor Sample.
"""
species = sample.atom_types
weights = NeutronScatteringLengths(species)
weighted = get_weighted_sample(sample, weights)
q_norms = np.linspace(0, q_max, n_points)
smeared = get_spherically_averaged_sample_smearing(
weighted, q_norms, q_width=q_width # in rad/Å
)
# Finally, compute the total dynamic structure factor Sqw by summing the weighted coherent Sqw_coh and the incoherent Sqw_incoh.
Sqw = smeared.Sqw_coh + smeared.Sqw_incoh
smeared.Sqw = Sqw
return smeared
weighted_and_averaged = weight_and_average_sample(sample, q_max=12, q_width=0.01, n_points=400)
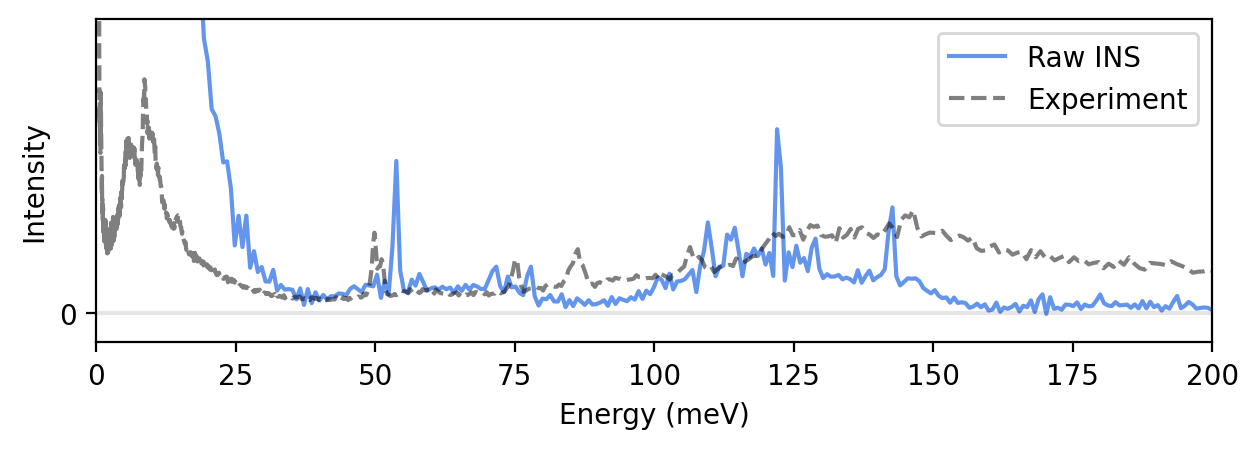
We can now plot the “raw” simulated inelastic neutron scattering spectrum by averaging the dynamic structure factor \(S(q, \omega)\) over \(q\). Note that we skip plotting the elastic line \(S(q, \omega=0)\) as the intensity is very large compared to the rest of the spectrum.
We also plot experimental data from Lindgren et al. for comparison. The experimental data is available in the archive reduced-benzene-tosca.zip on Zenodo, and is also available in the tutorials/ folder in the GitLab repository.
[12]:
from dynasor.units import radians_per_fs_to_meV
from scipy.optimize import minimize
# Load experimental data
cm_to_mev = 123.98419 / 1e3 # 1/cm -> meV
exp = np.loadtxt('data.benzene-tosca-Skoro-Rudic-2019-original-127K', skiprows=1, delimiter=',')
experiment_spectrum = exp[:, -2]
experiment_energy = exp[:,0] * cm_to_mev
def scale_spectrum(simulation, simulation_energy, experiment, experiment_energy, min_energy, max_energy):
#indices = np.argsort(np.abs(simulation_energy - selected_energy))
indices = np.argwhere((simulation_energy < max_energy) & (simulation_energy > min_energy))
interpolated_experiment = np.interp(simulation_energy, experiment_energy, experiment)
min_obj = minimize(fun=lambda x, spectra, ref: np.mean((x[0]*spectra - ref)**2),
x0=[1],
args=(simulation[indices], interpolated_experiment[indices]))
return simulation*min_obj.x[0]
ins_raw = np.nansum(weighted_and_averaged.Sqw, axis=0)
energy = weighted_and_averaged.omega * radians_per_fs_to_meV
ins_raw = scale_spectrum(ins_raw, energy, experiment_spectrum, experiment_energy, 25, 200)
fig, ax = plt.subplots(figsize=(7.2, 2.1), dpi=200)
ax.plot(energy[1:], ins_raw[1:], c='cornflowerblue', label='Raw INS')
ax.plot(experiment_energy, experiment_spectrum, c='k', linestyle='--', alpha=0.5, label='Experiment')
ax.axhline(0, c='k', alpha=0.1)
ax.set_xlabel('Energy (meV)')
ax.set_ylabel('Intensity')
ax.set_yticks([0])
ax.legend(loc='upper right')
ax.set_xlim([0, 200])
ax.set_ylim([-1, 10]);
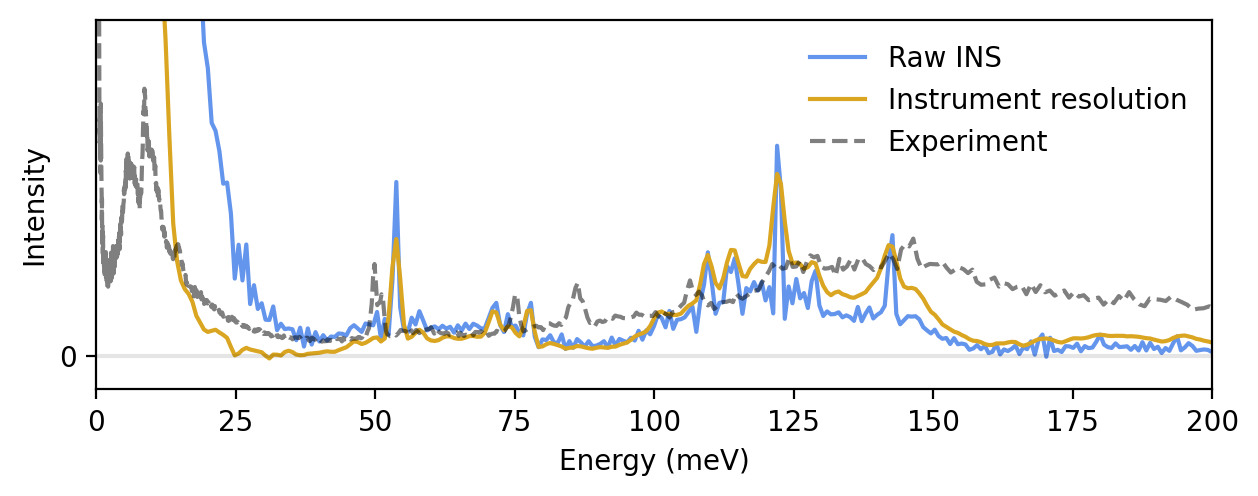
Apply experimental kinematic constraint and resolution function
The simulated INS spectrum above does not agree that well with experiments. In order to obtain a good agreement, we need to consider the actual instrument at which the experiment was performed, as well as compensate for the classical statistics from molecular dynamics simulations.
As stated previously, in this case we compare to experimental data measured at the TOSCA spectrometer at the ISIS Neutron and Muon Source in the UK. We use the euphonic and resINS packages to apply the instrument resolution and kinematic constraint.
[13]:
from euphonic import ureg
from euphonic.spectra import Spectrum1D, Spectrum2D, apply_kinematic_constraints
from resolution_functions.instrument import Instrument
from scipy.signal import fftconvolve
def resolution_function(sample: DynamicSample, instrument_string: str):
q_norms = sample.q_norms
e = radians_per_fs_to_meV * sample.omega
Sqw = sample.Sqw
q_norms_spacing = np.mean(np.diff(q_norms))
q_norm_bin_edges = np.concatenate([[q_norms[0] - q_norms_spacing/2], q_norms + q_norms_spacing/2])
bin_widths = np.diff(q_norm_bin_edges)
e_spacing = np.mean(np.diff(e))
e_bin_edges = np.concatenate([[e[0] - e_spacing/2], e + e_spacing/2])
spectrum = Spectrum2D(x_data=q_norm_bin_edges*ureg("1/angstrom"),
y_data=(e_bin_edges * ureg("meV")),
z_data=Sqw*ureg("dimensionless"))
spectrum.y_data_unit = "meV"
instrument = Instrument.from_default(instrument_string)
if instrument_string == "TOSCA":
res_function = 'AbIns'
E_FINAL = 3.97*ureg("meV")
E_INITIAL = None
# Technically the two detector banks of TOSCA corresponds to the angles 35 and 135 degrees.
# However, we use two slightly larger angle ranges in order to obtain better statistics.
angle_range_1 = (30, 40)
angle_range_2 = (130, 140)
res_model_mev = instrument.get_resolution_function("AbINS", e_initial=E_INITIAL, e_final=E_FINAL).polynomial
broadened = spectrum.broaden(x_width=1e-1*ureg("1/angstrom"),
y_width=lambda e: res_model_mev(e.to("meV").magnitude) * ureg("meV"),
width_convention='std',
method='convolve')
constrained_1 = apply_kinematic_constraints(broadened, e_f=E_FINAL, angle_range=angle_range_1)
constrained_2 = apply_kinematic_constraints(broadened, e_f=E_FINAL, angle_range=angle_range_2)
def convolve(constrained):
# convolve with a Gaussian to simulate less sharp angles
# Multiply wiht a N(0, 1) and transform to energy units
def gaussian(slice, x):
# Convolute a slice of Sqw with a Gaussian
smear = 0.5 # 1/Å or meV
mu = x[np.argmax(slice)] # center the convolution gaussian on the maximum intensity
angular_smearing = np.exp( - (x - mu)**2 / (2*smear**2) )
return fftconvolve(slice, angular_smearing, mode='same')
non_nan = np.nan_to_num(constrained.z_data.magnitude, nan=0.0)
q = constrained.x_data.magnitude
w = constrained.y_data.magnitude
conv = np.apply_along_axis(gaussian, 0, non_nan, q) # Apply convolution along q
return conv
convolved_intensity_1 = convolve(constrained_1)
convolved_intensity_2 = convolve(constrained_2)
kinematic_Sqw = np.nan_to_num(constrained_1.z_data, nan=0.0) + np.nan_to_num(constrained_2.z_data, nan=0.0)
#kinematic_Sqw = convolved_intensity_1 + convolved_intensity_2
kinematic_Sqw[kinematic_Sqw == 0.0] = np.nan
#kinematic_Sqw = broadened.z_data
# Sum the results from the two banks
constrained = Spectrum2D(
x_data=broadened.x_data,
y_data=broadened.y_data,
z_data=kinematic_Sqw*ureg("dimensionless")
)
Sqw = constrained
# Set x and y points to be bin centers instead of edges
Sqw.x_data = q_norms * ureg("1/angstrom")
Sqw.y_data = e * ureg("meV")
# Compute 1D sample
# Numpy will throw a warning regarding nanmean here, which we suppress.
with warnings.catch_warnings():
warnings.simplefilter("ignore", category=RuntimeWarning)
Sw = Spectrum1D(x_data=e * ureg("meV"), y_data=np.nanmean(Sqw.z_data, axis=0))
return Sw.y_data.magnitude, Sw.x_data.magnitude
ins_instrument, _ = resolution_function(weighted_and_averaged, "TOSCA")
[14]:
ins_instrument = scale_spectrum(ins_instrument, energy, experiment_spectrum, experiment_energy, 25, 200)
fig, ax = plt.subplots(figsize=(7.2, 2.4), dpi=200)
ax.plot(energy[1:], ins_raw[1:], c='cornflowerblue', label='Raw INS')
ax.plot(energy[1:], ins_instrument[1:], c='goldenrod', label='Instrument resolution')
ax.plot(experiment_energy, experiment_spectrum, c='k', linestyle='--', alpha=0.5, label='Experiment')
ax.axhline(0, c='k', alpha=0.1)
ax.set_xlabel('Energy (meV)')
ax.set_ylabel('Intensity')
ax.set_yticks([0])
ax.legend(loc='upper right', frameon=False)
ax.set_xlim([0, 200])
ax.set_ylim([-1, 10]);
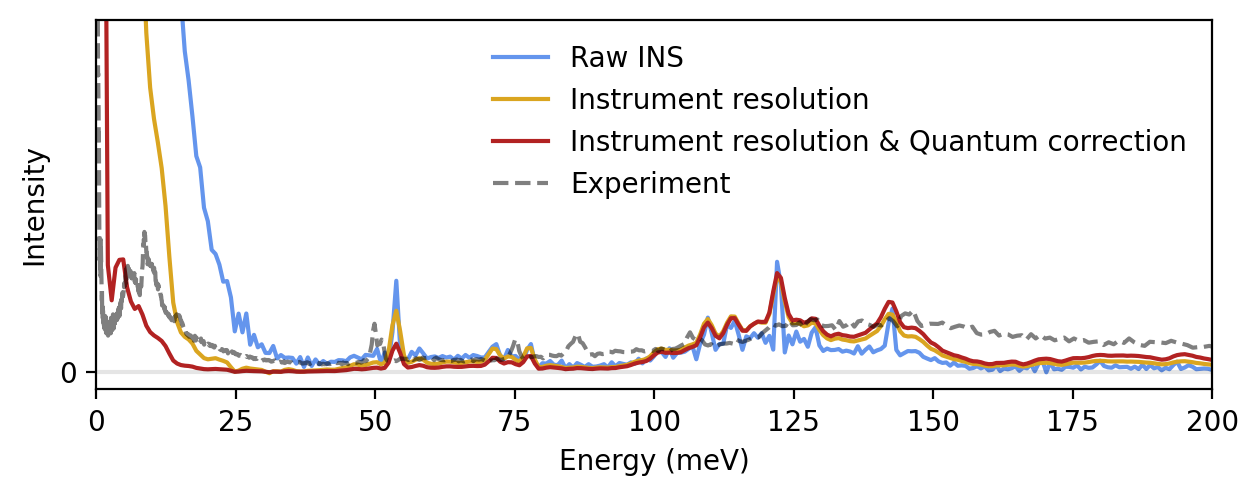
Finaly, we compensate for the classical statistics from molecular dynamics simulations by applying a first-order correction factor from perturbation theory. With the correction, we arrive at a semiquantitative prediction of the INS spectrum for crystalline benzene. The remaining red-shift of about 25 meV is attributed to the DFT functional used to train the NEP model. For more information about the correction as well as an extended discussion on the red-shift, please refer to the paper mentioned in the introduction of this tutorial.
[15]:
from ase.units import kB
def first_order_quantum_correction(energy_in_meV, T):
"""
Calculates a quantum correction to the classical MD statistics.
The correction is equal to the Bose-einstein distribution.
Returns a correction in meV.
The first order correction is
corr(e) = beta * e * [n(e) + 1]
= beta * e / (1 - exp( -beta*e ) )
n(e) = 1 / ( exp(beta*e) - 1 )
"""
epsilon = 1e-12 # To avoid division by 1
e_eV = energy_in_meV * 1e-3 # to eV
beta = 1 / (kB * T) # 1/eV
expon = np.exp( - (e_eV + epsilon) * beta )
denominator = 1 - expon
correction = beta * e_eV / denominator
return correction
def apply_first_order_quantum_correction(simulated, simulated_energy, temperature):
correction = first_order_quantum_correction(simulated_energy, temperature)
return simulated*correction
ins_instrument_and_quantum = apply_first_order_quantum_correction(ins_instrument, energy, temperature)
[16]:
ins_instrument_and_quantum = scale_spectrum(ins_instrument_and_quantum, energy, experiment_spectrum, experiment_energy, 25, 200)
fig, ax = plt.subplots(figsize=(7.2, 2.4), dpi=200)
ax.plot(energy[1:], ins_raw[1:], c='cornflowerblue', label='Raw INS')
ax.plot(energy[1:], ins_instrument[1:], c='goldenrod', label='Instrument resolution')
ax.plot(energy[1:], ins_instrument_and_quantum[1:], c='firebrick', label='Instrument resolution & Quantum correction')
ax.plot(experiment_energy, experiment_spectrum, c='k', linestyle='--', alpha=0.5, label='Experiment')
ax.axhline(0, c='k', alpha=0.1)
ax.set_xlabel('Energy (meV)')
ax.set_ylabel('Intensity')
ax.set_yticks([0])
ax.legend(loc='upper right', frameon=False)
ax.set_xlim([0, 200])
ax.set_ylim([-1, 20]);
Below is a production-grade simulation of the INS spectrum for benzene from the preprint by Lindgren et al. (2025). The structure was equilibrated using path-integral molecular dynamics (PIMD) for 500 ps, with production for 1 ns in the NVE ensemble. The system consisted of a 11x9x12 supercell for a total of 57024 atoms.