Thermal conductivity from BTE

Here, we provide an introductory tutorial on how to use phono3py to compute the thermal conductivity using a neuroevolution potential (NEP) via the Boltzmann transport equation (BTE). The system under study is graphite represented by a NEP model developed in this paper. Note that phono3py also allows you to compute other phonon properties such as, e.g., phonon lifetimes.

All models and structures required for running this and the other tutorial notebooks can be obtained from Zenodo. The files are also available in the tutorials/ folder in the GitLab repository.

Workflow

The steps required are:

1. Relax the primitive cell

2. Compute the force constants (fc2.hdf5, fc3.hdf5) using the NEP model for all structures generated by phono3py

3. Run the thermal conductivity calculation

Since phono3py does not have a python API we will call it through its command line interface via the os.system function.

BTE computational parameters

Note 1: In order to achive converged force constants one must use a sufficiently large supercell, the size of which is specified via the --dim option. Here, we, however, use a rather small supercell in order for the tutorial to run faster.

Note 2: Here, we use the phono3py default displacement amplitude of 0.03 Å when generating supercells for the force-constant extraction. This may not be suitable for every materials.

Note 3: In order to achieve convergence of the thermal conductivity one should use a larger q-point mesh (--mesh), but here we use a rather small mesh in order for the tutorial to complete within an acceptable time.

Note 4: In order to obtain accurate predictions for the thermal conductivity in graphite one should employ the --lbte (see here for more information). This method is, however, more costly both computationally and with respect to memory. For simpliticity we therefore limit ourselves to the relaxation time approximation (RTA), which is invoked via the --bterta option.

Miscellaneous

Additional related tutorials can be found on the hiphive website and here.

import os
import shutil
from glob import glob

import numpy as np
import h5py

from ase import Atoms
from ase.io import read, write
from calorine.calculators import CPUNEP
from calorine.tools import relax_structure
from matplotlib import pyplot as plt

from phono3py import Phono3py
from phono3py.interface.phono3py_yaml import Phono3pyYaml
from phonopy.interface.calculator import read_crystal_structure
from phono3py.file_IO import write_fc2_to_hdf5, write_fc3_to_hdf5

Preparations

We start out by setting up the working directory for the phono3py calculations.

root_dir = os.getcwd()  # here we set the root directory
work_dir = os.path.join(root_dir, 'phono3py_workdir')
shutil.rmtree(work_dir, ignore_errors=True)  # Deletes current working dir
os.mkdir(work_dir)
os.chdir(work_dir)

print(f'Root directory: {root_dir}')
print(f'Working directory: {work_dir}')

Root directory: /home/elindgren/repos/calorine/tutorials
Working directory: /home/elindgren/repos/calorine/tutorials/phono3py_workdir

Relaxation of primitive cell

First, we relax the primitive graphite unit cell (4-atoms) with respect to ionic positions and cell metric. To obtain accurate force constants it is recommended to use a tight convergence condition, i.e., a small value for the termination condition fmax.

potential_filename = os.path.join(root_dir, 'nep-C.txt')
prim = read(os.path.join(root_dir, 'graphite-prim.xyz'))
prim.calc = CPUNEP(potential_filename)
relax_structure(prim, fmax=1e-5)

Construction of force constants

Next, we construct the force constants. Here, we use the approach implemented in phono3py, which generates the second and third force constants by systematic enumeration and numerical evaluation of the derivatives involved. Especially for more complex materials, say systems with larger unit cells and/or lower symmetry, it can be beneficial to use regression based approaches such as the one implemented in, e.g., hiphive.

First, we call phono3py using the Python API to generate a series of configurations (supercells) with systematic displacements.

### supercell size
dim = (4, 4, 2)

write('POSCAR', prim)

ph3yml = Phono3pyYaml() # use phono3py api to generate the displacement dataset
unitcell, _ = read_crystal_structure("POSCAR", interface_mode='vasp')
ph3 = Phono3py(unitcell, supercell_matrix=dim, primitive_matrix='auto')

# Generates displacements for both second- and third order force constants.
ph3.generate_displacements()
ph3.save("phono3py_disp.yaml")
disp_dataset = ph3.dataset
supercells = ph3.supercells_with_displacements

Next we compute the forces for the second- and third-order force constants.

forces_data = []

def read_PhonopyAtoms_to_ase_Atoms(fname: str):
    """Convert from PhonopyAtoms to Atoms"""
    structure = Atoms(symbols=fname.symbols,
                  positions=fname.positions,
                  cell=fname.cell,
                  pbc=True)
    return structure


for it, fname in enumerate(supercells):
    structure = read_PhonopyAtoms_to_ase_Atoms(fname)
    structure.calc = CPUNEP(potential_filename)
    forces = structure.get_forces()
    forces_data.append(forces)
    if it % 100 == 0:
        print(f'FC3: Calculating supercell {it:5d} / {len(supercells)}, f_max= {np.max(np.abs(forces)):8.5f}')
forces_data = np.array(forces_data).reshape(-1, 3)
np.savetxt('FORCES_FC3', forces_data)

FC3: Calculating supercell     0 / 1220, f_max=  1.80689
FC3: Calculating supercell   100 / 1220, f_max=  1.80689
FC3: Calculating supercell   200 / 1220, f_max=  1.80690
FC3: Calculating supercell   300 / 1220, f_max=  1.80674
FC3: Calculating supercell   400 / 1220, f_max=  1.80693
FC3: Calculating supercell   500 / 1220, f_max=  0.44409
FC3: Calculating supercell   600 / 1220, f_max=  1.52169
FC3: Calculating supercell   700 / 1220, f_max=  1.80192
FC3: Calculating supercell   800 / 1220, f_max=  1.79870
FC3: Calculating supercell   900 / 1220, f_max=  1.80219
FC3: Calculating supercell  1000 / 1220, f_max=  1.80143
FC3: Calculating supercell  1100 / 1220, f_max=  1.07451
FC3: Calculating supercell  1200 / 1220, f_max=  1.80332

We then generate the force constants

forces = np.loadtxt('FORCES_FC3').reshape(-1, len(ph3.supercell), 3)
ph3.dataset = disp_dataset
ph3.forces = forces

ph3.produce_fc2() #generate fc2.hdf5
write_fc2_to_hdf5(ph3.fc2) #write fc2.hdf5
ph3.produce_fc3() #generate fc3.hdf5
write_fc3_to_hdf5(ph3.fc3) #write fc2.hdf5

BTE calculation

Having prepared the force constants we are now in a position to carry out the calculation of the lattice thermal conductivity. Note that the following cell can take a couple of minutes to run.

mesh = [16, 16, 8]  # q-point mesh
ph3.mesh_numbers = mesh
T_min, T_max = 10, 1000  # temperature range
T_step = 10  # spacing of temperature points

print("Start calculating BTE using Phono3py")
ph3.init_phph_interaction()
ph3.run_thermal_conductivity(temperatures=range(T_min, T_max + T_step, T_step),
                             write_kappa = True)

Start calculating BTE using Phono3py

After the calculation has concluded, we return to the original directory.

os.chdir(root_dir)

Analysis of results

We can now read the results of the BTE calculations from the kappa-<mesh>.hdf5 file (where <mesh> specicifies the q-point mesh used for the calculation). For more information about the content of the kappa-<mesh>.hdf5 file see here.

fobj = h5py.File(f'{work_dir}/kappa-m{mesh[0]}{mesh[1]}{mesh[2]}.hdf5')
print('Data:')
for key in fobj:
    print(f'  {key:25} : array-shape {fobj[key].shape}')

temperatures = fobj['temperature'][:]
kappa = fobj['kappa'][:]
gamma = fobj['gamma'][:]
freqs = fobj['frequency'][:]
fobj.close()

Data:
  frequency                 : array-shape (150, 12)
  gamma                     : array-shape (100, 150, 12)
  grid_point                : array-shape (150,)
  group_velocity            : array-shape (150, 12, 3)
  gv_by_gv                  : array-shape (150, 12, 6)
  heat_capacity             : array-shape (100, 150, 12)
  kappa                     : array-shape (100, 6)
  kappa_unit_conversion     : array-shape ()
  mesh                      : array-shape (3,)
  mode_kappa                : array-shape (100, 150, 12, 6)
  qpoint                    : array-shape (150, 3)
  temperature               : array-shape (100,)
  version                   : array-shape ()
  weight                    : array-shape (150,)

Here, kappa is an array of shape (number of temperatures, 6), where the 6 indices corresponds to the xx, yy, zz, yz, xz, and xy elements of the thermal conductivity tensor.

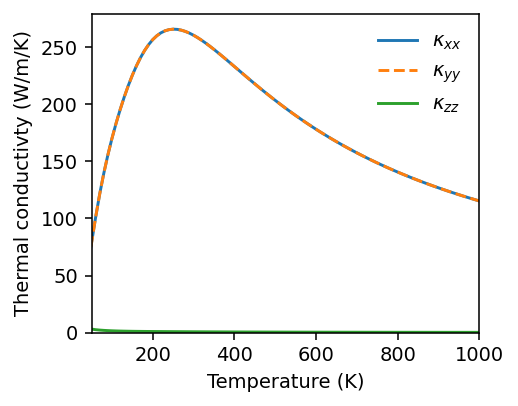
For the temperature dependence of the thermal conductivity, we obtain the following.

fig, ax = plt.subplots(figsize=(3.8, 3), dpi=140)

ax.plot(temperatures, kappa[:, 0], '-', label=r'$\kappa_{xx}$')
ax.plot(temperatures, kappa[:, 1], '--', label=r'$\kappa_{yy}$')
ax.plot(temperatures, kappa[:, 2], '-', label=r'$\kappa_{zz}$')
ax.legend(loc='upper right', frameon=False)

ax.set_xlim([50, temperatures.max()])
ax.set_ylim([0, np.max(kappa)*1.05])

ax.set_xlabel('Temperature (K)')
ax.set_ylabel('Thermal conductivty (W/m/K)')

fig.tight_layout()

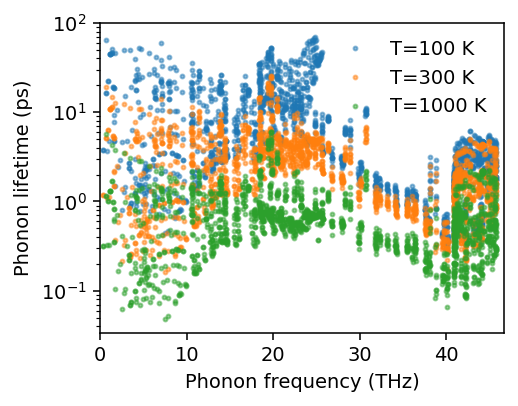
Similarly, we can visualize lifetimes.

fig, ax = plt.subplots(figsize=(3.8, 3), dpi=140)

T_index = 29
T_indices = [9, 29, 99]
for T_index in T_indices:

    print(f'Temperature {temperatures[T_index]}')
    g = gamma[T_index].flatten()
    g = np.where(g > 0.0, g, -1)
    lifetimes = np.where(g > 0.0, 1.0 / (2 * 2 * np.pi * g), np.nan)

    ax.semilogy(freqs.flatten(), lifetimes, 'o', label=f'T={temperatures[T_index]:.0f} K', alpha=0.5, markersize=2)

ax.legend(loc='upper right', frameon=False)
ax.set_xlabel('Phonon frequency (THz)')
ax.set_ylabel('Phonon lifetime (ps)')

ax.set_xlim([0, freqs.max()*1.02])

fig.tight_layout()

Temperature 100.0
Temperature 300.0
Temperature 1000.0